借助因果推断，更鲁棒的机器学习来了

资料仓库  收藏
0 / 1088

借助因果推断，更鲁棒的机器学习来了！

117 人赞同了该文章


导语

因果发现是在满足某些假设时，从数据中找出变量间因果联系。然而若是真正引起因果关系的变量本身就没有被观测到，那该怎么办？

从数据中提取对指定任务有帮助的特征，正是机器学习成功的原因。通过结合机器学习，可以在更少的假设下，发现因果关系。而借由找出的因果链条，则可以提升机器学习算法的泛化能力。

本文基于凯风研读营郭若城的分享，从以上两方面概述机器学习和因果推断间的关联。郭若城是美国亚利桑那州立大学博士，他的综述“A Survey of Learning Causality with Data:Problems and Methods”对该话题给出了全面的讲解。

自9月20日（周日）开始，集智俱乐部联合北京智源人工智能研究院还将举行一系列有关因果推理的读书会，欢迎更多的有兴趣的同学和相关研究者参加，一起迎接因果科学的新时代。该文的作者郭若城也会在读书会期间再详细具体深入地介绍机器学习和因果推断这个主题系列读书会详情与参与方式见文末。

1. 强忽略假设与混杂因素偏差

机器学习的任务，通常是描述式或预测式的，不需要涉及对数据本身因果关系的判断。然而近期的一些列方法学上的进展，使得能够基于更少的先验假设，境界基于大数据，从中学到因果联系。尽管这些方法，并没有直接地判别因果关系，但为因果推断指出了新的可能探索方法。
只使用观察到的数据，那能拿到的只是变量之间的条件概率分布以及联合概率分布，例如下图所示的，不同的人在吃药或没吃药时的健康状况，而要想推断出吃药和健康状况之间是否存在因果关系，可以看成是根据概率信息，计算平均干预影响（ATE average treatment effect）。

图1 观察到的数据实例
为了确保该问题是可解的，需要假设该问题中，所有可能同时对结果和原因产生影响的变量，都已被观测，且所有可能对结果产生影响的干预发生的概率在0到1之间，这被称为强忽略假设（Strong ignorability），这意味着只有给定了不同干预下的概率分布，就可以计算不同干预下的潜在可能结果的统计量。

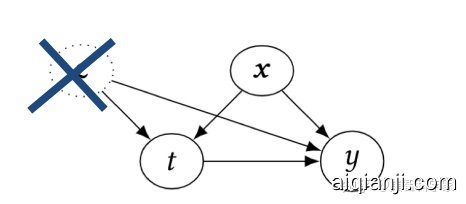图2 强忽略假设示意图，即可能的干扰变量c不存在
通常，强忽略假设是很难在真实场景下满足的。为此，可以通过隐含变量，即假设能够通过机器学习，提取隐变量。使得即使在混杂变量不可被观察时，通过控制隐变量，来将因果推断变为可解的统计问题。

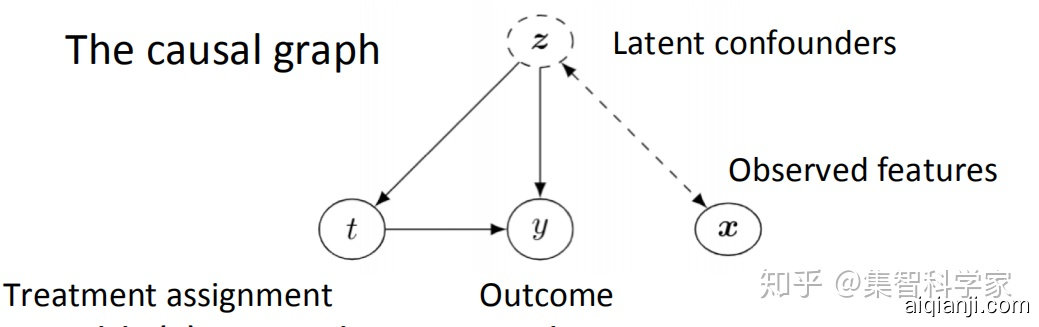图3 加入隐变量之后的结构因果图，图中的z可通过机器学习模型获得##

2. 三类判别因果关系的机器学习方法

第一类判断因果关系的方法，基于神经网络,同时认为强忽略假设满足。这类方法通过隐含层提取出的表征，代表了混杂因素。之后通过不同潜在结果下对应的神经网络，将隐变量的影响分别进行映射，最终得到不同干预下的损失函数，用以代表因果关系。

图4 CRFNet 网络结构图[1]
第二类方法，不要求强忽略假设满足，但假设变量间独立同分布。其代表是因果效应变分自编码器（CEVAE）[2]。该方法在假设隐变量z符合高斯分布时，通过最小化原因x和结果y的经过自编码器提取特征后差异，通过深度神经网络表征隐变量z，之后可依据学到的模型，做反事实推断。

图5 CEVAE模型示意图
第三类方法，基于树模型，要求强忽略假设满足，例如因果随机森林，模型学习如何通过将变量所处的空间，进行划分，逐渐地从整体的概率分布，得到具体场景下的干预影响，从而估计异质环境下的影响，以此来间接地评价因果关系。

在社交网络中，相互有联系的个人，往往在众多未被观测到的特征上，有着相似性，这被称为同质性（homophily）。因此，在使用机器学习进行因果推断中，如果能考虑社交网络间的连接，能够在强忽略假设不满足时，更好的估计隐变量。

图6 基于图卷积网络，提取社交网络的特征，结合原数据特征。使用表征平衡损失，以平衡干预与否状况下的潜在混杂因素分布[3]。##

3. 无偏差的机器学习

该如何选择机器学习算法的评价指标？或者问什么样的指标能够避免过拟合？对这两个问题的回答，可以从下图的对比看出。

图7 因果推断vs机器学习 对比图 [5]
左图的乌鸦，之所以能够通过将碎石放入瓶中，从而喝到水，这是由于其理解了这背后的因果关系。而右图的鹦鹉，训练者需要的是其学会人类的语言，但实际考察的，却只是其模仿人类语句的能力。

而不涉及因果的机器学习，正如同这个鹦鹉，只是学会了如何做出使评价指标提升的决策，却没有考虑这样的选择和最终的需求之间是否存在因果联系。尤其是当测试数据与验证数据分布不同时，则更可能出现过拟合。

例如在工业界使用机器学习来提升商品总销量（GMV），在算法开发时，使用的是离线的数据集及评价指标，在算法上线后，通过实时数据进行评估。这里有两个挑战。一个是算法线上表现和公司商业表现的关系尚不清楚。一个模块（如推荐系统）更好的线上表现可能并不能使公司盈利增加，因为它可能同时导致其他模块（如搜索）的表现下降。

第二个是我们无法直接使用线上表现的标签训练机器学习模型。这是因为正在训练的模型和已经上线的模型在预测上的不同带来的偏差。如何无偏差地利用已经上线的模型搜集到的数据去离线场景下训练新的模型也是一个因果机器学习中重要的问题，这个问题又被称为无偏差机器学习。

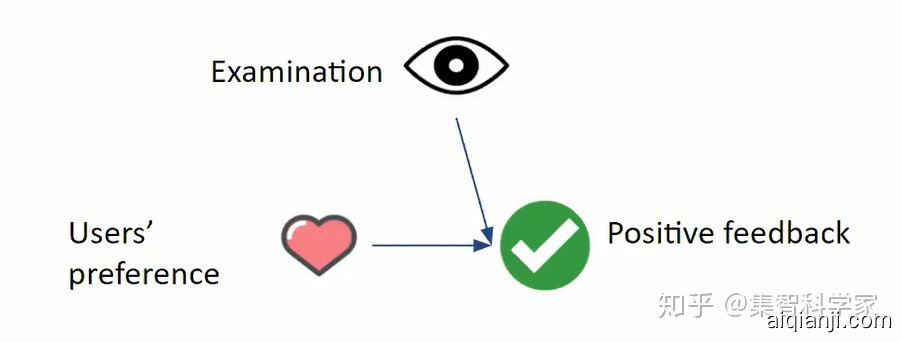图8 离线评价，在线评价与真实商业场景下表现的对比和联系 [5]
然而，如果使用在线的数据进行评测，往往会对用户的体验造成影响。A/B测试意味着用户会看到不同的展示界面。而无偏差的机器学习的目标，则是不进行在线评测，根据算法在离线数据上的评价指标，来估计其在真实商业场景中的效果。

图9 影响用户点击的因素包含展示方式和用户喜好
例如，搜索中，排在前的网页被点击得更多，用户点击网站有两个先决条件，用户看到网站，同时还喜欢网站，如果排序算法对网站的评分，没有考虑当前网页排名带来的影响，就会在评估时有偏。然而推荐算法真正想提取的，是用户喜好的信息。

而相比传统的网页搜索，电商网站的搜索结果，往往会以二维的网格呈现，这使得电商搜索数据呈现带来的偏差与传统的网页搜索相比，变得更为复杂，为此在通过用倾向性得分 (Inverse Propensity Scoring) 来对标签进行加权。去校正选择性偏差前，需要根据离线数据或者在线随机实验，评估每个标签（点击或者购买）对应的倾向性得分。

例如，之前的研究指出，触屏中，如果用户对展示的这几项都不感兴趣，则不会看完而会直接滑动换一屏；对屏幕中间展示的商品更容易关注，相比线性的展示，用户的注意力能停留更长时间。而通过实际数据检验，发现对展示位置为的中间商品的偏好不存在，因此在之后，就不需要考虑针对这一偏差，使用Inverse Propensity Score IPS 进行权重再分配。

4. 如何学习不同环境下的相同特征

数据标签和待学习的特征，往往存在着伪关联。例如训练集中骆驼的图片都出现在沙漠中，而羊的图片都出现在草原，如此训练出的模型，会将沙漠的特征当成骆驼的特征，然而这并非是存在着因果关系的特征。

将特征分为两类，一类为因果特征，一类为伪特征。因果特征能够跨越不同的数据类型，在不同的场景下迁移。而后者会随着数据所属范畴的改变而改变。能够提取出因果特征的模型，泛化能力更强。

根据是否找到代表因果关系的特征，可以将训练好的深度学习模型分为是否具有异分步可泛化性（OOD ：out of distribution ）。如果模型的训练数据，来自从多个来源收集的独立同分布的数据，且测试数据和训练数据不同，则称模型具有OOD泛化能力。

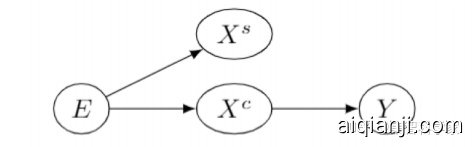图10 因果不变特征示意图
上图中数据E，经由因果特征Xc，影响分类标签Y，而Xs为伪相关特征。在数据E的范畴改变时，给定E是Xc和Xs的分布都会改变，而给定Xc得出标签Y的分布不变，因此将Xc称为表征了因果联系的特征。论文[4]中提出的IRM方法，详述了如何捕捉因果不变特征。

该文在二分类问题中，在训练集和测试集中，加入了颜色和标签之间的伪相关，并使得训练集和测试集之间的之间颜色的分布相反。如下图中左边测试集中，相同标签的数字图片多为绿色，而测试集中的图片为红色。对于IRM，其在训练集和测试集中的分类准确度远高于传统模型，接近了去掉颜色这一干扰因素的理想情况。

图11 颜色呈不同分布的训练和测试数据集
然而，IRM作为一种正则项，虽然能够学到因果联系，但不适用于高维数据，且在优化过程中，引入了额外的复杂性。

5. 总结

从数据中发现因果关系，按对数据的假设，可以分为假设数据独立同分布，数据不满足独立同分布，但强忽略假设满足，以及包含未观察到的隐变量三种。机器学习相关的方法，主要试图解决后一种问题。而传统因果发现中基于约束或打分模型的方法，需要实际中更难满足的强忽略假设。

图12 因果推断和机器学习的方法汇总图
从数据中发现因果关系的方法汇总，左边的子树对应从数据中学习包含未观测隐变量的因果联系的强弱，中间代表如何学习因果关系的方向，右边代表了因果性和机器学习方法的关联[6]。

经由因果性特征的发现，除了帮助模型具有更好的迁移能力，具有异分布泛化性，还能够用于半监督学习及强化学习。未来可能的研究方向还包括如何提升模型的可解释性，以及让模型更加公平，例如对少数族裔或女性不进行“算法杀熟”。

而在另一个方向上，即通过寻找特征，间接地寻找因果关系及其影响程度。如何应对高维的数据、时序数据，如何处理结果与原因之间存在的环状结构等，仍然是开放问题。然而对于同样发源于统计的机器学习和因果推断，两者之间的方法学，注定存在可借鉴之处与更多值得进一步研究的联系。

参考文献：
[1] Johansson, Fredrik, Uri Shalit, and David Sontag. "Learning representations for counterfactual inference." International conference on machine learning. 2016.

[2] Louizos, Christos, et al. "Causal effect inference with deep latent-variable models." Advances in Neural Information Processing Systems. 2017.

[3] Guo, Ruocheng, Jundong Li, and Huan Liu. "Learning individual causal effects from networked observational data." In Proceedings of the 13th International Conference on Web Search and Data Mining, pp. 232-240. 2020.

[4] Arjovsky, Martin, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. "Invariant risk minimization." arXiv preprint arXiv:1907.02893 (2019)

[5] Wang, Zenan, Xuan Yin, Tianbo Li, and Liangjie Hong. "Causal Meta-Mediation Analysis: Inferring Dose-Response Function From Summary Statistics of Many Randomized Experiments." In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 2625-2635. 2020.

[6] Guo, Ruocheng, et al. "A survey of learning causality with data: Problems and methods." ACM Computing Surveys (CSUR) 53.4 (2020): 1-37.

作者：郭瑞东
审校：郭若城
编辑：邓一雪
https://zhuanlan.zhihu.com/p/260834457

相关性≠因果性

在阐述为什么之前需要阐述是什么？在日常生活和数据分析中，我们可以得到大量相关性的结论，我们通过各种统计模型、机器学习、深度学习模型，通过分析得到种种结论，但是这里面存在一个巨大的疑问就是，“相关性一定等于因果性吗？”

举个 ，这个是缅因州黄油消费量和离婚率的关系

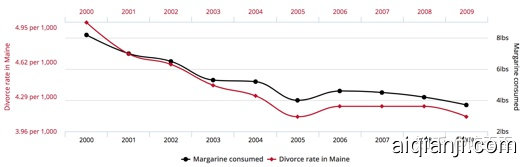从图上可以看出这两个变量呈高度相关的关系，但是如果我们从因果的角度来阐释，说黄油消费导致了离婚，或者离婚导致了黄油出售，显然都非常荒谬。

实际上，相关性通常是对称的，因果性通常是不对称的（单向箭头），相关性不一定说明了因果性，但因果性一般都会在统计层面导致相关性。

为什么需要因果推断

举个 ，我目前在做权益方向的工作，以权益为例，我们为了促进某些不活跃用户的消费，给不活跃用户发了更大的红包，给活跃用户发了更小的红包，把所有特征扔进模型训练，得出了一个奇怪的结论，给用户越大的红包，用户越不买东西。

不考虑因果性的话，相似的或者别的类型的错误还有很多，《Theoretical Impediments to Machine Learning With Seven Sparks from the Causal Revolution》这篇论文说到了因果推断的三层

第一层是关联：X条件下Y会怎么样，也就是现在机器学习中常用的方式，尽可能通过深层次的网络去拟合X和Y的关系

第二层是干预：如果我服用了阿司匹林，身体会怎么样？也就是如果我改变了X，Y会怎么样？

第三层是反事实推断：相当于对结果来考虑原因，相当于如果我们希望Y变化，那么我们需要对X做出什么样的改变？

从作者角度这样看来，因果推断是高于现行机器学习方法的方法，但我的观点来说，因果推断的方法其实是通过因果关系，解决现行只考虑相关关系的的机器学习方法产生的一系列问题。

因果推断研究的两个问题——从辛普森悖论讲起

上图男女分别来看

  • 女性对照组1/(1+19)=5%发病率，处理组3/(3+37)=7.5%发病率，这个药对女性有害
  • 男性对照组12/(12+28)=30%发病率，处理组8/(8+12)=40%发病率，这个药对男性也有害 但从总体看，对照组13/(13+47)=21.6%发病率，处理组11/(11+49)=18.3%发病率，这个药对人类有效，发生了什么？

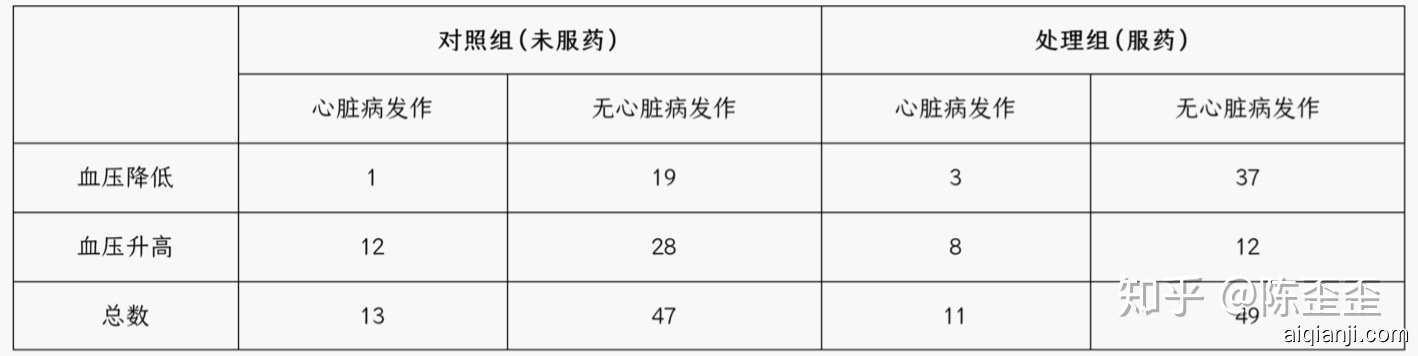上图分血压情况来看

  • 血压降低的情况下对照组1/(1+19)=5%发病率，处理组3/(3+37)=7.5%发病率，血压降低的患者发病率增加了
  • 血压升高的情况下对照组12/(12+28)=30%发病率，处理组8/(8+12)=40%发病率，血压升高的患者发病率也增加了 但从总体来看，对照组13/(13+47)=21.6%发病率，处理组11/(11+49)=18.3%发病率，这个药对人类有效，发生了什么？ 让我们来看两种情况下的因果图

从上面的因果图可以很容易明白

在第一个问题下，不同的性别有不同的服药意愿，也就是性别是服药和发病的共同原因，所以应该分层进行统计

在第二个问题下，服药会导致血压变化，也就是血压是服药和发病的共同结果，如果分层统计，则会低估服药的影响，总体的结论才是正确的。

从这两个辛普森悖论的例子我们可以看出现在因果推断最重要的两个研究方向：

  1. causal discovery：因果发现，也就是发现以上统计变量之间的因果关系，从统计变量中探寻出一个如上的因果图
  2. causal effect：因果效应，在得到因果关系之后，确定效果，比如上面的问题是，知道因果图之后，确定服药之后发病率增加（减少）多少

注：后面的介绍主要还是着重于因果效应相关的论文和发展，如果对于因果发现更有兴趣的大佬可以移步。

基本概念

这里用到了我在实际业务上的假设，这里的权益干预可以看做是任何一种干预，比如广告，推荐list等等。

基础方法

随机试验——因果推断的黄金准则

Y1(x)，Y0(x)表示个体i接受治疗的个体因果作用，但是对于单个个体来说，要么接受treatment，要么不接受，Y1(x)，Y0(x)中必然会缺失一个，但在T做随机化的前提下，我们可以识别总体的ATE：

这是因为

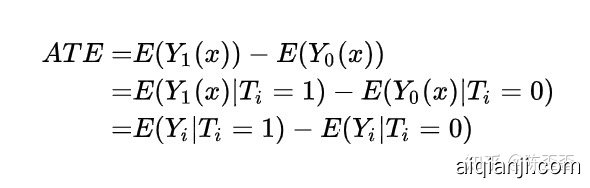最后一个等式表明ATE可以由观测的数据估计出来。其中第一个等式用到了期望算子的线性性(非线性的算子导出的因果度量很难被识别!);第二个式子用到了随机化，即 T⊥(Y(1), Y(0))(⊥表示独立性)

可以看出，随机化实验对于平均因果作用的识别有着重要作用。

但是实际应用中，随机化实验是最“贵”的因果推断方式，有时候我们无法控制“treatment”，更多时候成本实在太高，我们只能拨一小波人进行实验，所以这种“黄金标准”并不算实用。

双重差分法（difference in difference DID）

在随机试验那部分我们提到，可以采用ATE = E(Yi|Ti=1)−E(Yi|Ti=0)的前提是T⊥(Y(1),Y(0))，那如果不符合这个条件应该怎么办？有一个比较老且基础的方法是双重差分法，也就是差分两次。

这张图讲得非常清楚，首先为什么我们不能用ATE = E(Yi|Ti=1)−E(Yi|Ti=0)，举个 ，我们给一些人发权益，另一些人不发，我们怎么能知道权益带来的购买效果是怎么样的呢？简单的方法就是给发权益的人购买数加和，不发权益的人购买数加和，然后两个加和相减就好啦，但是如果这两部分人本来不发权益的时候购买数就不一样呢？

那就减两次，从上图来说，我们把这两群人发权益之前t0的购买数相减，得到一个差值，相当于这两群人的固有差距，再把这两群人发权益之后t1的购买数相减，相当于这两群人被权益影响之后的差距，后面的差距减去前面的差距，就会得到权益对于差距有多少提升（降低），以此作为权益的effect。

这个方法的问题在于有个比较强的要求是，趋势平行，也就是要求t0到t1之间，两群人的购买概率变化趋势是一样的（图中那个平行线），这其实是一个很强的假设，所以这个方法我个人来讲不算非常认可。DID之上还有DDD，也就是多组别多时间点的DID，在此不多赘述。

从matching到倾向性得分

随机化试验那部分我们讲到了

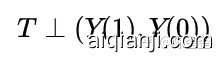这个公式其实包含了较强的可忽略性（Ignorability）假定，但我们之前说了，这种方式比较“贵”，所以通常我们会希望收集足够多的X，使得：

如果看过一些因果论文的同学会知道，这个叫Conditional Independence Assumption (CIA) 这是因为

那么这个方法实际操作起来通常就是称之为Exact matching，也就是对于每一个 =1的用户，我们从 =0的分组里找一个变量 一模一样的用户，在这个X的条件下，满足T与Y相互独立，此时直接比较两组用户观察结果 的差异就可以得到结论，但是，“匹配用户的变量 完全相等” 这个要求过于严格，不实用。

由此衍生了用倾向性得分进行匹配的方式Propensity Score Matching，简称 PSM：在 PSM 方法中，我们首先对每一个用户计算一个倾向性得分（propensity score），定义为 e(x)=Pr(T=1 | X=x) ，这里面的假定由T⊥(Y(1),Y(0)) | X变为了T⊥(Y(1),Y(0)) | e(x)，接着我们根据倾向性得分对于用户进行匹配。

但是这种方式也是有其局限性的，就是在于treatment group和control group的用户需要足够齐全且维度较高，实际应用的时候我们会发现本身两个group的用户有较明显的差异，想要找到倾向性得分相近程度达到要求的用户非常难。

相关的方法非常多：

  • 用倾向性得分来对用户进行分组，称为 subclassification
  • 用倾向性得分来对用户进行加权抽样，称为 Inverse Propensity Score Weighting (IPSW) ，权重为

### 树模型

代表的算法有BART，Causal Forest，upliftRF 。

以2018年的《Estimation and Inference of Heterogeneous Treatment Effects using Random Forests》为例，这篇论文主要讲了Double sample trees和propensity trees，在此只简单介绍propensity trees，整体的流程如下：

其实整体思路非常清晰，就是训练一棵预测treatment的树，然后在树的叶子结点做因果推断，如果大家仔细看了前面的倾向性得分的话，会发现其实这个思路其实就相当于propensity matching的树版，可能跟subclassification更相似。

关于因果推断的树模型方式理论上应该专门开一栏进行介绍，但是相关论文我看的不多，而且在很多因果推断的新论文里面BART，Causal Forest的效果其实都比不上现在新的前沿算法了，所以在此就简单介绍一种。

相关的因果推断方向还有很多，比如重加权方法，表示学习方法，对抗学习方法，doubly robust方法，元学习方法等，这些方向相关论文都不少，如果都在这篇里面说完会显得全文非常冗余，所以后期会尽量把相关看过的论文都总结下来。

开源工具

这里面照搬了综述文章《A Survey on Causal Inference》里面的图，其实讲的已经非常全了，大家自行食用：

推荐资料

授人以鱼不如授人以渔，所以这里也把自己推荐的资料列出来给大家，都是综述总结类的资料，对于在领域内深挖应该有一些帮助。

meta learning

这个方向使用基础的机器学习方法去首先Estimate the conditional mean outcome E[Y|X = x]（CATE），然后 Derive the CATE estimator based on the difference of results obtained from step 1，我们常见的uplift model里面one model和two model方法其实也是属于meta learning，在这个领域one model方法是所谓的S-learner，two model方法是所谓的T-learner

  1. T-learner & S-learner

这里不多赘述这两种方法，简单来讲，T-learner就是用分别的两个base learner去模拟干预组的outcome和非干预组的outcome，优点在于能够很好地区分干预组和非干预组，缺点则在于容易出现两个模型的Bias方向不一致，形成误差累积，使用时需要针对两个模型打分分布做一定校准，S-learner是将treatment作为特征，干预组和非干预组一起训练，解决了bias不一致的问题，但是如果本身X的high dimension可能会导致treatment丢失效果。而且这两种方法更偏向于naive的方法，很多其他的问题比如干预组和非干预组样本不均衡的问题、selection bias的问题都未解决。

2. X-learner

在这两种方法的基础之上还有《Metalearners for estimating heterogeneous treatment effects using machine learning https://www.pnas.org/content/116/10/4156》这篇论文中介绍的X-learner

首先跟T-learner一样，用base learner去预估干预组和非干预组的response

然后定义

这里D的定义为response的预估值和实际值的差值，然后我们用一个estimator去预估这里的D，最终我们的CATE就是这两个预估出来的τ的加权和。

论文中用图来解释了这么做的原因，如下：

如上图所示，如果我们的干预组和非干预组样本数量不均衡，如图A的蓝色，那么在预估蓝色的base learner时会出现无法拟合到中间上凸部分的情况，最终得到的treatment effect就是在中间部分下凸的结果。

但是如果我们使用了imputed treatment effect，会得到C中虚线的均衡结果。

论文中还提到了自己的实验，实验效果总结来看，如果treat和不treat的数据量差别比较大的时候，X learner效果特别好，但是如果CATE接近0的时候，X learner效果不如S learner，比T learner好，make sense的。

3. 总结性论文

meta learning的方法有非常多，这里只是提到较为经典的三种，其他meta learning的方法比如R-learner有点老了，这里不再介绍，在《Transfer Learning for Estimating Causal Effects using Neural Networks https://arxiv.org/abs/1808.07804》中比较有意思的是提到了很多方法的方案，包括传统艺能S-learner，T-learner，X-learner和比如warm start T-learner、joint training等等，有兴趣可以看看。

representation learning

表示学习对于因果推断其实算是非常自然的想法，本身由于selection bias的存在，导致treament group和control group的人群自带偏差，而类似S-learner的方法又会使得treat的作用丢失，那么将人群embedding中并尽可能消除bias和保存treat的作用就非常重要了。

  1. BNN & BLR

比较经典的论文有BNN、BLR《Learning Representations for Counterfactual Inference https://arxiv.org/abs/1605.03661》，整体的算法如图：

其中B指的是loss：

loss包含了三部分：事实数据的误差+和与i最近的j的反事实数据的误差和事实数据+反事实数据的分布差异，那我们是怎么学习φ的呢？

一个方法是对于特征进行选择BLR，在embedding层只有一层，更加白盒，相当于特征筛选，只保留在treatment group和control group差距较小的特征。

另一个方法是深度的方法BNN，embedding后整体的loss加入分布的差异。

2. TARNet

与这篇论文很相似的论文包括TARNet《Estimating individual treatment effect:generalization bounds and algorithms https://arxiv.org/abs/1606.03976》，这篇文章整体的思路跟BNN那篇有点像，说到了BNN那篇的问题，这里面讲了BLR的两个缺点，首先它需要一个两步的优化（优化φ和优化y），其次如果如果φ的维度很高的话，t的重要性会被忽略掉，挺有道理的，但感觉跟那篇唯一的区别就是解决了一下treat和control组的sample数量不均衡的问题，所以火速看了一下就过了

loss的计算为：

可以看出是在上篇论文的基础上增加了ω的加权，去除了样本不均衡的问题。整体的算法步骤如下：

把两步走的优化变为了同时优化，虽然优化看起来比较微小，但如果大家实际跑一下IHDP数据集的话会发现提升还是挺明显的。

3. CFR

还有一篇论文是在TARNet之上进行优化的，《Counter Factual Regression with Importance Sampling Weights https://www.ijcai.org/Proceedings/2019/0815.pdf》而本文的改进点也在ω上，不除以p(t)，而是用一个网络学习了p(t|x)，除以p(t|x)

作者将其简化为

可以用任何的网络去拟合第二项，整体的过程为：

4. ACE

还有一篇论文讲到了另一个角度《Adaptively Similarity-preserved Representation Learning for Individual Treatment Effect Estimation http://www.cs.virginia.edu/~mh6ck/papers/ICDM2019Liuyi.pdf》

这篇主要的思想希望在representation之后能够尽可能地保留local similarity，用一个toy example来说如下：

整体的框架如图：fprop(x)是提前训练好的倾向性得分function

整体希望representation之前用x计算出倾向性得分相近的两个个体，representation之后，representation之间的距离还是相近，把最重要的部分贴下来如下：

其中Q是Ri和Rj的联合概率（R是representation），P是xi和xj的联合概率，similarity preserving loss就是Q和P的KL散度，其中S的函数如下：

整体的loss包括正常的imbalance loss：

Factual y的分类或者回归loss：

还有similarity preserving loss，总的loss function就是：

5. SITE

还有一篇比较类似思想的论文是SITE《Representation Learning for Treatment Effect Estimation from Observational Data https://papers.nips.cc/paper/7529-representation-learning-for-treatment-effect-estimation-from-observational-data.pdf》但这篇论文我没有非常认真地读，来自NIPS，也是非常经典的一篇，说的主要是普通的representation learning的方法考虑了全局的分布信息，但是没有考虑用户间的局部相似性，然后KNN的方法考虑了局部相似性，但是忽略了全局信息，这里面用了三元triplet pairs的方法选择三个对，用的是倾向性得分，倾向性得分在中间的一对，倾向性得分接近1的treat unit，倾向性得分接近0的control group，有兴趣的同学可以自己看一下。

xiaogalayy