介绍
这篇文章包括三部分:第一部分介绍相关和因果的区别以及我们为什么需要因果关系,第二部分介绍因果关系的定义,第三部分介绍怎么从数据中判断出因果关系。
希望大家读后能对因果推断有初步的了解,在分析数据时有意识地想一下是否存在因果关系。但这次分享无法提供一个稳定得出因果关系的方法,而是提供思路和工具,帮助我们更好地处理这类问题。
Why
相关≠因果/correlation does not imply causation
人均巧克力消费量与诺贝尔奖比例:

参考网站:http://www.tylervigen.com/spurious-correlations


xkcd
因果关系有什么用?
基于相关可做出准确度很高的预测,但不能直接指导决策,因果关系则可以指导我们做决定。
例子:假设我们有酒店价格和入住率的历史数据,且酒店价格由基于入住率的算法自动实现,入住率高就提价。那么,机器学习算法能够识别出价格和入住率的正相关,即已知价格时,可以准确地预测入住率。但如果我们想知道提价对入住率的影响,用这套算法却会得出“提价能多卖出更多房间”的结论,这好像违背了经济学常识。此时,我们就需要用另一种方法来解答这个问题。
同样的数据可以对应多种不同的数据生成过程,从数据本身无法判断真正的数据生成过程,但可以用作预测。
我们可以回忆一下历史上用来预测天体轨迹的日心说和地心说模型。托勒密的地心说模型的预测精度非常高,却是完全错误的。
更贴近业务来看下预测模型用于决策会有什么问题,比如流失率预测的例子:在很多公司经常需要对可能流失的用户做干预,从而减少流失率。因为资源有限,所以一般做法是用过去的流失客户做样本训练一个识别客户流失概率的模型,然后针对最容易流失的客户做干预,但这么做并不一定是高效的。原因很简单,虽然我们可以很好地预测客户的流失概率,但是预测并不是我们的目的。我们的目的是为了通过干预减少流失率,所以要找的是干预带来留存提升最大的客户群体,而这部分客户未必是最容易流失的客户。因此,要想真正实现有效的干预,就不能靠准确预测流失率的算法,而要想办法找到干预后最有效果的客户,但后者靠通常的预测算法不一定能得到。
另一个例子是搜索广告有效性的评估。eBay曾经不区分相关与因果,建了一个用点击来预测成交的简单模型,发现搜索广告的回报率高达1400%;然而用实验方法来衡量真实的回报率时,发现只有-63%。之所以差别这么大,是因为那些会点广告的人即使没有广告也会去eBay买东西。所以,衡量广告的真实回报要看广告对效果的提升,而不是看广告行为后续的效果本身。
小结
上面几个例子都是在说明我们面临的很多决策问题不能通过预测模型来回答。实际工作中,数据分析师的很多工作都是辅助决策,其实不止数据分析师,只要是需要从数据中得到结论的场景,经常就需要超越简单的相关关系,去努力搞清楚事物之间的因果联系,这样才能做出高质量的决策。

What
什么是因果关系?
前面虽然没有明确定义因果关系,但我们对什么是因果关系其实有很好的直觉。
因果关系试图回答的是what-if的问题:其他不变,如果改变A后,Y的取值改变,则AY有因果关系,A 导致了Y。
其他不变这个前提要求我们想象一个反事实的场景,在常用的因果模型里叫做潜在结果(Potential Outcome)。我们用手术来举例,假如A - 是否手术,Y - 1年后能否存活,那每个个体都有两个潜在结果,一个是接受手术后的结果,一个是不接受手术后的结果。这两种结果之间的差别就是手术和存活的因果关系。
但现实中我们只能观察到个体的某一个潜在结果,所以个体粒度的因果关系是很难确定的。这个难题被称作因果推断的根本难题,本质上是一个缺失数据(missing data)的问题,但缺失的这部分数据是不可能搜集到的。
假设我们全知全能,看到了平行宇宙中的选择,知道每个个体在不同处理方式下的结果,那么就不受这个问题困扰。
全知全能的情况:

全知全能的情况
但实际上:
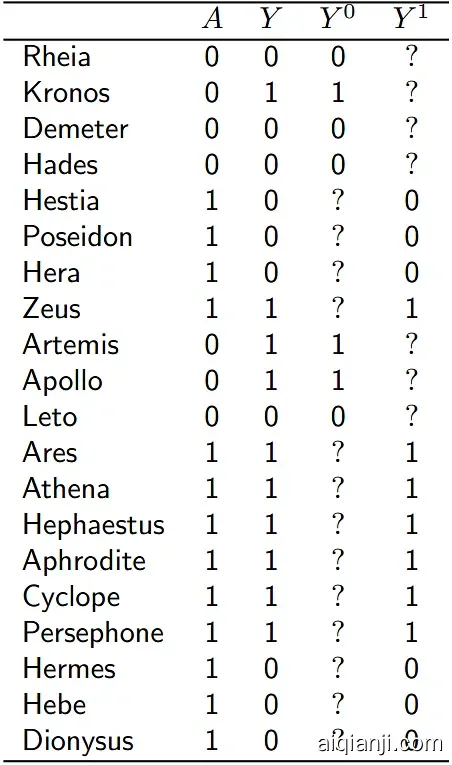
实际情况
我们只能观察到同一个个体在一种操作下的结果,我们观察不到what if。
小结:相关和因果的区别
了解因果关系的定义后,可以用一张图解释因果关系和相关关系的区别:

How
A/B实验: gold standard of causal inference
如果我们不关注个体粒度的因果关系,只关注整体的平均因果效应,则随机试验可以完美解决这个问题,业务上的问题基本上都属于这类。
为什么随机可以解决:随机可以保证两组用户的潜在结果一致。随机试验的实质在于分配机制(用户分流)与潜在结果无关,现实中可能影响每个人潜在结果的因素很多,其中很多观测不到,我们不需要关心,随机分组本身就保证了它和潜在结果无关。换言之,实验组/对照组可交换,每组的潜在结果可以认为是整体的潜在因果,因此可以直接对比得出因果效应(假设样本量接近无限,忽略抽样方差)。
这就是互联网公司为什么重视A/B实验,因为它可以提供其他方法很难提供的因果效应,从而指导决策。我们常说的数据驱动,不是有数据就可以驱动,需要A/B实验这样的结果数据才能更好地驱动,不然数据驱动的决策也可能是很糟糕的决策。
如何从观察数据中推断因果关系?
随机实验虽好,但不是所有场景都可行(需要考虑成本/伦理/可行性等)。那么可以从观测数据中推断因果关系吗?从前面的例子可以知道,不能直接推断,但也有方法。
假设/业务理解的重要性:以辛普森悖论为例
因果推断的前提是比较同样或者说可比较的对象。在随机试验中,这一点是通过随机分流实现的;但在观测数据里没有随机这个过程,要用别的办法。这时最重要的是从已有的知识出发,得出可信的假设,即哪些因素会影响到我们关心的X和Y;再根据这些假设建立因果模型,以推断因果关系。比如冰淇淋销售量和游泳溺水的人数相关,如果我们确定同时影响两者的变量只有温度,那就可以比较同样温度下两者是否仍然相关,由此得出因果关系。
在实际工作中,这些假设就是我们对业务的理解,这是好的数据分析工作的前提。用xx之前说的一句话,“要用业务来解释数据,而不是用数据来解释数据”。
为什么只从数据无法得出结论?
分性别看数据:应该吃药。这时要看分性别数据,而不是汇总数据。

分性别看数据
分血压看数据:不应该吃药。这时要看汇总数据,而不是分血压的数据。

分血压看数据
同样的数据,结论为何不同?什么时候要看总体,什么时候又要分维度看数据?
因果关系的识别(Identification)与估计(Estimation)
识别:根据假设和观测数据判断是否可以从中估计出因果关系,这个过程是判断一个因果效应能否用观测数据表示出来;
估计:在因果关系可识别的前提下,从观测数据中计算出因果效应大小的方法。
下面讲的DAG特别适合用来识别。估计效应大小经常要用传统的统计学方法或机器学习方法;但同样是多元回归,预测数据或估计因果时选择变量的逻辑不一样,预测只需要选提高预测准确度的变量,估计因果要根据预设的因果方向来确定。
DAG:把假设可视化呈现
DAG简介
Directed Acyclic Graph (有向无环图)是把假设可视化呈现的一种工具,用来判断在什么情况下可以识别因果关系,以及如何识别因果关系。
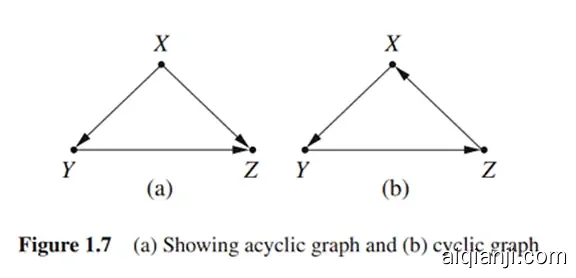

以分析机票价格和售出率的关系为例:(左上的a图)设Y是价格,Z是售出率,X是影响需求的其他变量(比如是否假日)。简单起见,我们认为除了X没有其他变量同时影响Y和Z,这种情况下要计算AY/Z之间的因果关系,就需要控制X,即在X固定的情况下看Y/Z之间的相关性。
在这种简单场景下,看图就可以知道应该控制哪些变量。在更复杂的情况下,DAG有一套规则来确定应该控制哪些变量。
DAG是假设的可视化,它使得假设更清晰,推理过程更明确。如果没有假设,我们无法直接从数据得出应该控制哪些变量。产出同一份数据的可能过程是很多的,不同的数据生成过程要求控制不同的变量来得到因果关系。因此如果只从数据出发,我们不可能知道哪一种做法是对的。
需要注意的是在画DAG时,每一条线都是一个因果称述,缺失的线同样重要,同样是因果判断。
后门法则
这是在图里确定控制哪些变量的一个法则,控制这些变量就可以得出因果效应(前提是图本身是对的)。步骤是列出所有变量间的路径,确认哪些是后门路径,然后看需要控制哪些变量能关闭这些路径,在图比较复杂的情况下更有用。
用DAG看辛普森悖论
性别是混杂变量,所以要分性别看数据:
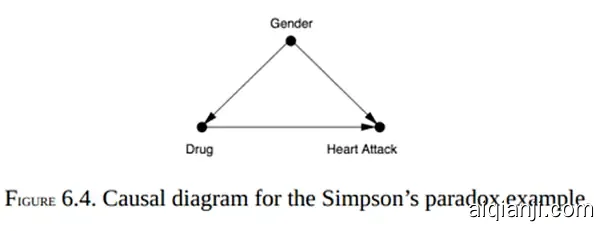
血压是药物发生作用的中介变量,所以不应该分血压看数据:

在实际问题上,因果关系可能没有这么明显。比如Google做的关于性别薪酬不平等的一项研究,结论是在同样的职位上,女性的薪酬更高一些。这样的结论合理吗?如果我们认为性别会影响获得管理职位的可能性,那比较同样职位的做法就是不准确的。

两种Bias
混杂偏差(confounding bias):Common causes

混杂偏差很常见,也比较容易被发现,这种偏差主要出现在有些变量不容易或不能被观察到的场景中。比如我们分析发现游戏转化人群中,近期有过多次转化的用户在单个游戏中的留存低于只转化一次的人群,那是否意味着我们加上转化保护后留存情况会提升?有可能但不一定,因为有过多次转化的用户和只有一次转化的用户在用户特征上不一样,而这会影响留存,只看观测数据我们无法判断转化保护的效果,因为不能直接找出可比较的用户,但我们还有随机实验,类似的还有dislike用户活跃或留存更高,有过转化行为的用户的留存/活跃更高。
选择偏差(selection bias):Conditioning on common effects

幸存者偏差即是选择偏差的一种。
招聘的案例:假设是否通过面试取决于两点:简历和能力,两者都不行的话会被刷掉,两者都很好的可能付不起工资,这样的话通过面试的人就是所有人群中的一小部分,这部分人里简历和能力的负相关就是选择偏差导致的,不足以指导决策。
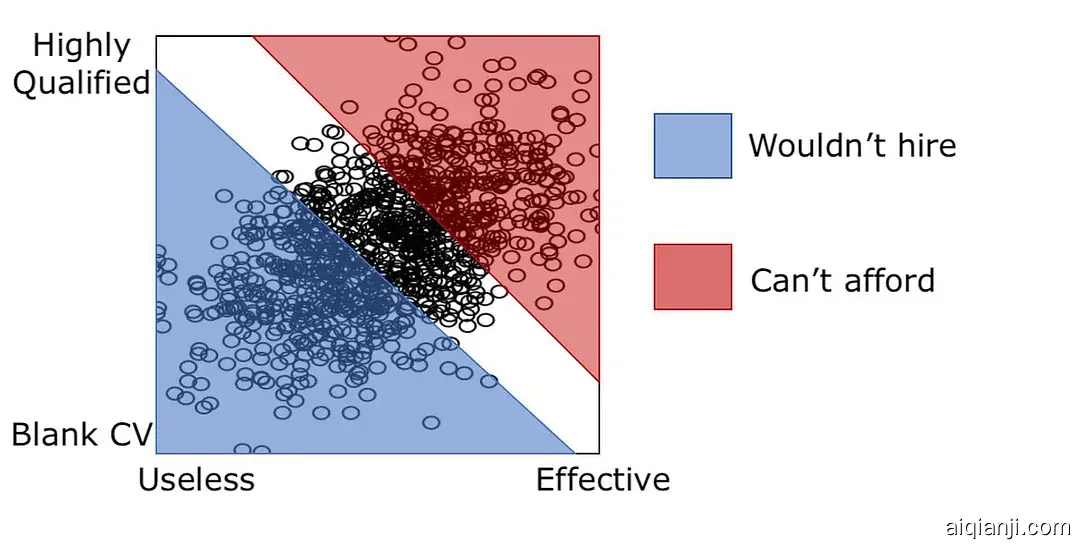
比如X-颜值Y-智商,Z-是否结婚:

这种场景很常见,比如新奇的科学发现大概率不能被重复,比如演技与颜值的相关。在广告系统里,我们看到的后验数据会受到各种因素的影响,因此选择偏差非常常见。比如计划出价和CVR的关系,在看到的数据里可能是负相关的,但这不是因为出价和CVR之间有因果关系,而是能跑出来的计划要么是出价够高要么CVR够高,只有这样预估ecpm才可能胜出。我们常说后验数据有偏,也是在说投放出来的数据不是全部数据,这对数据分析是很大的挑战,因为我们无法知道没投出来的广告的后验数据。
小结
这部分介绍了获取因果关系的常用方法和常见偏差,除了随机实验外,利用DAG可以从观测数据推断因果关系,除了DAG这种因果图的方法之外,统计学和计量经济学还发展出了断点回归/双重差分/工具变量/倾向值匹配等工具。
从观测数据推断因果关系的可靠性依赖于假设的合理性,在实际使用中推断出的因果效应可能存在较大偏差,比如FB一个衡量广告有效性的研究表明,从观测数据推断的因果效应和随机试验的结果存在较大diff,如下图:

https://www.facebook.com/business/news/insights/demystifying-measurement-why-methodology-matters
总结
- 相关关系适合预测,不适合指导决策;
- 因果关系依赖what if;
- 随机实验是因果推断的黄金准则;
- 从观测数据推断因果关系依赖假设/业务理解;
- DAG是一种可视化呈现假设的方法,且有一套规则来估计因果效应;
- 混杂偏差和选择偏差是最常见的两种偏差;
“More has been learned about causal inference in the last few decades than the sum total of everything that had been learned about it in all prior recorded history."
A “causal revolution” is upon us.
参考资料
- Causal inference in economics and marketing
- 辛普森悖论:如何用同一数据证明相反的论点
- Want to make good business decisions? Learn causality
- The Book of Why中文版
- Causal Inference in Statistics - A Primer
- Common Structures of Bias
- An Introduction to Directed Acyclic Graphs
- A Crash Course in Good and Bad Control
- Causation and Correlation
- Causal Diagrams: Draw Your Assumptions Before Your Conclusions
- Causal Inference: What If
- Tutorial on Causal Inference and Counterfactual Reasoning
- Don’t Put Too Much Meaning Into Control Variables
- Causal Data Science
- Beyond prediction: Using big data for policy problems
- Causal Reasoning: Fundamentals and Machine Learning Applications
- Using Causal Inference to Improve the Uber User Experience
- A Comparison of Approaches to Advertising Measurement
- An introduction to Causal inference
- A Revolution in Measuring Ad Effectiveness: Knowing Who Would Have Been Exposed
[深度]A/B 测试中的因果推断——潜在结果模型
对 A/B测试有了解的读者都知道,A/B测试通过用户分组进行在线试验,可以对比产品两个版本的方案找出哪一个更好。但是很多人可能会问:我为什么一定要用 A/B Testing?Google Analytics 这么强大,我的产品的用户访问一目了然,通过数据分析不难找到问题所在,A/B测试还有必要吗?

这篇文章里,作者将从因果关系方面仔细分析为什么在关键的产品决策时,您需要 A/B Testing,而不仅仅是 GA。
AB测试有两个隐含的前提:“稳定性假设”和“分配机制随机”,虽然线上互联网产品基本都满足这些设定,但是并不意味着AB测试能无往不利。在大量的场景下,稳定性假设和分配机制随机并不成立。
稳定性假设
稳定性假设通俗讲,就是测试环境和全量环境下,非实验条件是不变的。
常见的线上产品是用户自己使用,比如你刷抖音和别人刷抖音其实是互不干扰的,抖音修改了算法在20%用户下算法效果提升,在100%的用户下算法效果应该也是提升的。
但很多情况下用户之间是有关联的,比如滴滴的分单算法做了调整,一半的司机使用新算法,一半的司机使用旧算法,新算法的司机如果拿了更多的订单,就会影响剩余司机的绩效。不能把两类司机的绩效差值认为是新算法的效果。更有甚者,如果新算法的特点就是更容易抢老算法的订单,那么可能全量之后新算法效果不变或者下降。
总而言之,如果你通过所谓的随机分组之后,并不能保证稳定性假设成立,那么AB测试就会失效。
分配机制随机
分配机制随机意味着可以将用户分成随机组,保证其他因素的影响相同。问题是,能做实验的产品迭代其实是有限的。
类似按钮的样式、图片的样式、信息的排布格式这些可以AB测试,包括排序策略、召回策略、广告展示策略这些策略类也可以做AB测试。
然而这些调整简而言之就是规模比较小,对用户体验影响也并不重大。大部分重大的迭代,反而无法做测试。
比如会员权益,只能同时发布,否则一半用户没有会员权益会引起投诉。比如一系列的市场代言活动,无法进行分组测试,甚至用户无法追踪。比如商品定价策略,更不可能去做AB测试,否则一篇大数据杀熟的公众号能要了你的命。
解决方案
从数据中挖掘因果效应是近些年来计量经济学的重要方向,之前的学术研究聚焦在假设检验中,但是时代变了。在互联网时代,也许数据量不能支持所有的问题都机器学习一波流,但是达到均值差异置信是没问题的。在现在的情况下,因果关系的确认变得更加重要。在计量经济学中,有一个概念叫做潜在结果。如果一个用户被干预,会表现出行为A,不干预的潜在结果就是行为B,那么A-B的效益差就是干预变量带来的因果效应。
概念很简单,解决方案也很简单,就是找到潜在结果的估算方法。
AB测试的本质是拿对照组作为潜在结果。时间段前后分析是假设功能发布前后的其他因素稳定;时间片轮转测试,每隔1个小时用不同的策略,消除时间上的差异。这些是非AB测试之外的方法。另外回归算法也是一个好方法,可以通过回归确认某些因素对指标的影响。
相关性与因果关系
前面问题的回答从统计学上看很简单,GA 这种观察性的数据分析工具主要用于探索性的研究,它长于发现问题,而不是解决问题;它可以用来发现事物之间的相关性,但是很难用来确认因果关系。
在概率论和统计学中,相关(Correlation,或称相关系数),显示两个随机变量之间线性关系的强度和方向。
——维基百科
相关性在探索性的研究中是很有用的,它可以在实践中预示某种关系,指明进一步研究的方向。相关性的典型例子是产品的需求和价格的关系,空气质量和汽车数量的关系。这两个相关性的例子都暗示了更进一步的因果关系,因为从经济学上看价格下降会提升需求,汽车数量增加使得尾气排放量增加而导致空气质量变差。但是,不是所有的相关性都有因果关系,相关并不意味着因果。
15 Insane Things That Correlate With Each Other 这个网站收集了很多看起来很荒谬的相关性例子。
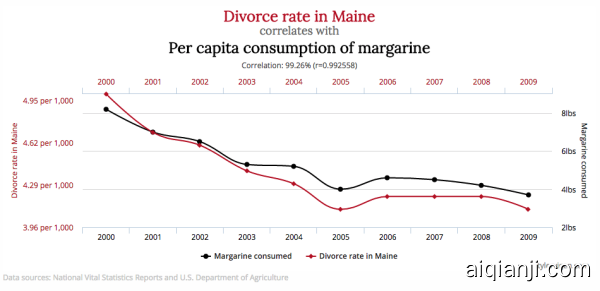
上面的例子中,美国缅因州的离婚率和人均黄油消耗量在 2000 年至 2009 年间达到了极强的相关性(相关系数 0.9926)。吃黄油和离婚明显是没有因果关系的两件事,因为根据我们的常识,吃多点黄油不至于让人性情大变而导致离婚,离婚之后也不太可能因为心情沮丧而多吃黄油。
如果我们的研究目的是找出缅因州离婚率下降的主因,人均黄油消耗量和离婚率之间的相关性有用吗?显然这个相关性的作用是很有限的,你不能据此得出结论:少吃黄油有助于婚姻和谐。我们希望得到的是和离婚率之间的因果关系,这就需要针对性的调查或试验。吃黄油和离婚两者表面上的相关性顶多起到提示性的作用(假如有的话),例如,研究人员可能会想到,是否有一个第三因素,导致了缅因州离婚率和黄油消耗量的共同下降,如经济形势?
因果关系在很多应用场合是我们的核心关注点,例如产品的优化方案。更醒目的 Call to Action 按钮是否会促进着陆页的转化?什么样的表单用户更愿意去完成?这些问题的背后都是一些 PM 需要去确证的因果关系,正是 A/B 测试可以大展身手的地方。
A/B 测试也称为在线对照试验 (Online Controlled Experiments) ,是一种科学地进行统计因果推断的研究方法,它和其他统计研究方法(如观察性研究)的主要区别在于它可以通过针对性的试验简单高效地对所考察的因素和变量间的因果关系进行科学地推断。
那到底什么是因果关系呢?
因果关系是一个事件(即“因”)和第二个事件(即“果”)之间的关系,其中后一事件被认为是前一事件的结果。一般来说,因果还可以指一系列因素(因)和一个现象(果)之间的关系。对某个结果产生影响的任何事件都是该结果的一个因素。
——维基百科
A/B 测试要研究的就是这种简单逻辑上的因果关系,而不是先有鸡还是先有蛋这种近乎哲学上的因果。确切地说,我们通过试验要证明的是:某个因素/处理是否会对某个现象/结果产生作用。

下面我们将根据统计学上的潜在结果模型,仔细分析因果关系的定义和推断过程。
潜在结果
首先明确一下统计学上因果关系的定义。在试验的上下文中,我们讨论的因果关系是和某个处理 (treatment) 关联在一起的,作用的目标主体是参加试验的个体。
一个或多个处理作用在个体上产生的预期效果我们称之为潜在结果 (Potential outcome)。之所以称为潜在结果是因为在一个个体上最终只有一个结果会出现并被观察到,也就是和个体所接受的处理相对应的那个结果。另外的潜在结果是观察不到的,因为它们所对应的处理并没有实际作用在该个体上。
举个例子,今天北京是重度雾霾天(很正常),你出门可能戴口罩了,也可能没戴口罩(忘了,很不幸!)。这个小试验的个体就是你,戴口罩和不戴口罩就是两个不同的处理。戴或者不戴,当然只能选一个,结果也只能观察到一个。如果你没有戴口罩,今天痛苦地咳嗽了 100 分钟(会不会挂掉?),你会很后悔地想:要是我今天记得戴口罩,那么我可能只会咳嗽 10 分钟。戴口罩的话你会咳嗽 10 分钟,不戴口罩的话你会咳嗽 100 分钟,咳嗽 10 分钟和 100 分钟分别就是这两个处理所对应的潜在结果。因为你实际上没戴口罩而咳嗽了 100 分钟,所以,这戴口罩只咳嗽 10 分钟的潜在结果只是你想象的结果,不是实际发生和观察到的。
听起来是不是有点反事实 (Counterfactual) 推断的味道?是的,潜在结果就是这种想象中的:假如我这几年买的是美股,而不是 A 股,那结果就是赚 100 万,而不是赔 100 万了(捶胸顿足)。
因果效果
在定义了潜在结果之后,不同的处理产生的因果效果 (Causal effect)就很清楚了,它就是不同潜在结果的比较。
