Causal Inference: Trying to Understand the Question of Why
[Mar 7, 2020·11 min read
*Why are you reading this article? *Why did you choose to learn about causal inference? Why are you thinking that this is a really weird way to start an article? Who knows. A more interesting question to ask is why can we, as humans, think about and understand the question “why” in the first place!? If we ever want to create a system with Artificial General Intelligence, or AGI, we need to answer this question.
*你为什么要读这篇文章?*你为什么选择学习因果推理?为什么你认为这是开始一篇文章的一种非常奇怪的方式?谁知道。一个更有趣的问题是,作为人类,我们为什么可以首先思考和理解“为什么”这个问题!?如果我们想创建一个具有通用人工智能或 AGI 的系统,我们需要回答这个问题。

understanding why requires understanding of the whats, the wheres, and the whens. The hows, however, seem to be an implementation of the whys. image source.You, and everyone else on this planet, are able to understand cause-and-effect relationships, an ability that is still largely lacking in machines. And before we can think about creating a system that can generally understand cause-and-effect, we should look at cause-and-effect from a statistics perspective: causal calculus and causal inference. Statistics is where causality was born from, and in order to create a high-level causal system, we must return to the fundamentals.
Causal Inference is the process where causes are inferred from data. Any kind of data, as long as have enough of it. (Yes, even observational data). It sounds pretty simple, but it can get complicated. We, as humans, do this everyday, and we navigate the world with the knowledge we learn from causal inference. And not only do we use causal inference to navigate the world, we use causal inference to solve problems.
你和 这个星球上的其他人都能够理解因果关系,在很大程度上机器仍然缺乏这种能力。在我们考虑创建一个可以大致理解因果关系的系统之前,我们应该从统计学的角度来看待因果关系:因果演算和因果推理。统计是因果关系的起源,为了建立一个高层次的因果系统,我们必须回归本源。
因果推断是从数据中推断出**原因的过程。任何类型的数据,只要有足够的数据。(是的,即使是观察数据)。这听起来很简单,但它可能会变得复杂。作为人类,我们每天都这样做,我们用从因果推理中学到的知识来探索世界。我们不仅使用因果推理来导航世界,还使用因果推理来解决问题。

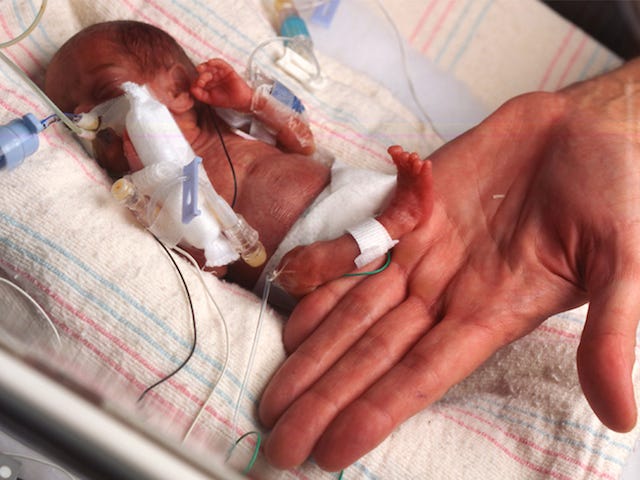
15 million premature babies are born every year. image source.Every year, 1.1 million premature babies die. In other words, 7.3**% **of all premature babies die every single year. Millions of parents have to struggle through the grief, suffering, and pain of losing their child over a process they can’t control. That’s a problem. Let’s say we want to figure out whether comprehensive treatment after the birth of a premature baby will affect its chances for survival. In order to solve this problem, we need to use causal inference.
The python library we’ll be using to perform causal inference to solve this problem is called DoWhy, a well-documented library created by researchers from Microsoft.
每年,有 110 万早产儿死亡。换句话说,每年有7.3 **%*的早产儿死亡。*数以百万计的父母不得不在他们无法控制的过程中经历失去孩子的悲伤、痛苦和痛苦。那是个问题。假设我们想弄清楚早产儿出生后的综合治疗是否会影响其生存机会。为了解决这个问题,我们需要使用因果推理。
我们将用于执行因果推理以解决此问题的 Python 库称为DoWhy,这是一个由 Microsoft 研究人员创建的有据可查的库。

A Quick Lesson on Causality
First, a quick lesson on causality (if you already know the basics, you can skip this section; if you prefer to watch a video, lucky you, I made one that you can watch here).
Causality is all about interventions, about **doing. **Standard statistics is all about correlations, which are all good and fun, but correlations can lead to wrong assumptions which can lead to a lot worse things.
关于因果关系的快速课程
首先,关于因果关系的快速课程(如果您已经了解基础知识,可以跳过此部分;如果您更喜欢观看视频,幸运的是,我制作了一个您可以在这里观看的视频)。
因果关系是关于干预的,关于**做的。**标准统计都是关于相关性的,这些都是好的和有趣的,但相关性会导致错误的假设,从而导致更糟糕的事情。
This is a graph showing the correlative relationship between Exercise and Cholesterol (which *looks like a causal relationship but is not). *If we just look at the correlative relationship between cholesterol and exercise, it looks like there’s a causal relationship between the two. But this correlation actually happens because both cholesterol and exercise share a common cause or confounder: age.
这是一个图表,显示了运动和胆固醇之间的相关关系(*看起来像因果关系,但实际上不是)。*如果我们只看胆固醇和运动之间的相关关系,看起来两者之间存在因果关系。但这种相关性实际上发生是因为胆固醇和运动都有一个共同的原因或混杂因素:年龄。
In correlations, the notation is P(x|y) i.e. the probability of x given y: for example, the probability of a disease given an active gene. However, in causal calculus, a very small but important change is made. **Instead of P(x|y) it’s P(x|do(y)) **i.e. the probability of x given that y is done: for example, the probability of a disease given that I start a diet. The ‘do’ is very important: it represents the intervention, the actual doing of something that will cause the effect.
在相关性中,符号是 P(x|y),即给定 y 的 x 概率:例如,给定活性基因的疾病概率。然而,在因果演算中,发生了一个非常小但很重要的变化。不是 P(x|y) 而是 P(x|do(y)) ,即给定 y 完成后 x 的概率**:例如,给定我开始节食的情况下发生疾病的概率。“做”非常重要:它代表干预,即实际做的事情会导致效果。**
If this ‘do’ stuff still isn’t making too much sense, let me take you through another example:
Take air-pressure and a barometer. There is a correlation between the reading on a barometer and the air-pressure, but, in a standard correlation (P(x|y)) we wouldn’t be able to tell which one caused which. However if we switched it up to causal calculus, otherwise known as do-calculus (yes, the ‘do’ is everywhere) we could ask a question like, “What is the probability of a high barometer reading given that the pressure increases?” Increasing the pressure is the act of doing, and through doing and intervening, we can see if there is a clear causal relationship between the two variables. (Clearly we would see an increase in the barometer reading if we increased the pressure).
This works vice-versa as well. If we changed the reading on the barometer (by twisting a knob or something, which is an act of doing) we would not see the air-pressure change because the barometer reading does not cause the air-pressure. The air-pressure affects the barometer reading.
如果这个“做”的东西仍然没有太大意义,让我带你看另一个例子:
测量气压和气压计。气压计上的读数与气压之间存在相关性,但是,在标准相关性 (P(x|y)) 中,我们无法分辨是哪个导致了哪个。但是,如果我们将其转换为因果演算,也称为 do-calculus(是的,'do' 无处不在),我们可以问这样的问题:“鉴于压力增加,气压计读数高的概率是多少?” 增加压力是做的行为,通过做和干预,我们可以看到两个变量之间是否存在明显的因果关系。(显然,如果我们增加压力,我们会看到气压计读数增加)。
反之亦然。如果我们改变了气压表读数(通过扭动旋钮或东西,这是一种行为做),我们将不会看到空气压力的变化,因为气压计的读数不会造成空气压力。气压会影响气压计读数。
air pressure -> barometer reading. source.
However, the air pressure and barometer example is pretty simple; there are only two factors. In real life, there are countless factors that each have some sort of causal relationship with the others.
然而,气压和气压计的例子非常简单;只有两个因素。在现实生活中,有无数的因素相互之间存在某种因果关系。



an example of a causal diagram. image source.In the diagram, “traffic jam” is a confounder or common cause for “late for school” and “long queues”. =Confounders are variables that have a causal relationship with two variables that we want to test a causal relationship between=**.** If we wanted to test the causal relationship between “late for school” and “long queues”, we would have to account for “traffic jam” in order to make sure of the validity of the causal relationship found between “late for school” and “long queues”, as in the cholesterol example of above. **In causal inference, we always need to account for confounders because they introduce correlations that muddle the causal diagram.**
在图中,“堵车”是“上学迟到”和“排长队”的混杂因素或常见原因。 =**混杂因素是与两个变量之间存在因果关系的变量,我们要测试它们之间的因果关系**=**. **如果要检验“上学迟到”和“排长队”之间的因果关系,就必须考虑“堵车”,以确保“上学迟到”和“大排长龙”之间因果关系的有效性。 “排长队”,如上面的胆固醇示例。**在因果推断中,我们总是需要考虑混杂因素,因为它们引入了混淆因果图的相关性。**
IHDP Dataset
Ok now that we have a good understanding of basic causality, let’s actually get to the code and test the causal relationship between the wellbeing of a premature twin and intervention. We’ll be using the dataset from the Infant Health and Development Program (IHDP) which collected data on premature infants in randomized trials in the US from 1985–1988. Randomization is key because it provides an unbiased account of the world. Because this data was collected in an RCT, causal inference is not necessary, but we will still do it to show how it works.
好的,现在我们对基本因果关系有了很好的理解,让我们实际进入代码并测试早产双胞胎的健康与干预之间的因果关系。我们将使用来自婴儿健康与发展计划 (IHDP) 的数据集,该数据集收集了 1985 年至 1988 年美国随机试验中早产儿的数据。随机化是关键,因为它提供了对世界的公正描述。因为这些数据是在 RCT 中收集的,所以不需要因果推断,但我们仍然会这样做以展示它是如何工作的。
An intensive intervention extending from hospital discharge to 36 months corrected age was administered between 1985 and 1988 at eight different sites. The study sample of infants was stratified by birth weight (2,000 grams or less, 2,001–2,500 grams) and randomized to the Intervention Group or the Follow-Up Group. The Intervention Group received home visits, attendance at a special child development center, and pediatric follow-up. The Follow-Up Group received only the pediatric follow-up component of the program.** Measures of cognitive development, behavioral status, health status, and other variables were collected from both groups** at predetermined time points…. The many other variables and indices in the data collection include site, pregnancy complications, child’s birth weight and gestation age, birth order, child’s gender, household composition, day care arrangements, source of health care, quality of the home environment, parents’ race and ethnicity, and maternal age, education, IQ, and employment. — from the HMCA archive.
1985 年至 1988 年间,在八个不同地点进行了从出院到矫正年龄 36 个月的强化干预。婴儿的研究样本按出生体重(2,000 克或更少,2,001-2,500 克)进行分层,并随机分配 **到干预组或随访组。**干预小组接受了家访、特殊儿童发展中心的出勤和儿科随访。随访小组仅收到该计划的儿科随访部分。从两组中收集认知发展、行为状态、健康状况和其他变量的测量在预定的时间点…… 数据收集中的许多其他变量和指标包括地点、妊娠并发症、孩子的出生体重和胎龄、出生顺序、孩子的性别、家庭组成、日托安排、医疗保健来源、家庭环境质量、父母种族和种族、母亲的年龄、教育、智商和就业。—来自HMCA 档案。
The Code
First, let’s import the required package and load the data.
首先,让我们导入所需的包并加载数据。
import dowhy
from dowhy import CausalModel
import pandas as pd
import numpy as npdata= pd.read_csv(“https://raw.githubusercontent.com/AMLab-Amsterdam/CEVAE/master/datasets/IHDP/csv/ihdp_npci_1.csv", header = None)col = [“treatment”, “y_factual”, “y_cfactual”, “mu0”, “mu1” ,]for i in range(1,26):
col.append(“x”+str(i))data.columns = col
data = data.astype({“treatment”:’bool’}, copy=False)
print(data.head())
____________________________________________________________________ treatment y_factual y_cfactual mu0 … x22 x23 x24 x250 True 5.599916 4.318780 3.268256 … 0 0 0 01 False 6.875856 7.856495 6.636059 … 0 0 0 02 False 2.996273 6.633952 1.570536 … 0 0 0 03 False 1.366206 5.697239 1.244738 … 0 0 0 04 False 1.963538 6.202582 1.685048 … 0 0 0 0
Treatment here is the intervention. Y_factual is the outcome, quantified through the combination of the mental, behavioral, and health statuses of the infants. All the x’s (x1 to x25) are confounders** **of the outcome and the intervention: variables like gender, race, quality of home-care, etc. **We’re trying to figure out the causal relationship between the treatment and the outcome, while accounting for the confounders. **(Technically we don’t have to account for these confounders because the data was collected through a randomized trial and any bias that would build up with them would be wiped out. However, it’s still a good idea to account for them, and it’s absolutely necessary to account for them when the data is observational).
We don’t care about y_cfactual, mu0, and mu1 (they’re used by the creators of the GitHub linked in the code (a super cool project on a Causal Effect Variational AutoEncoder, or CEVAE, that you should totally check out))
这里的治疗是干预。Y_factual 是结果,通过婴儿的心理、行为和健康状况的组合进行量化。所有 x(x1 到 x25)都是** **结果和干预的混杂因素:性别、种族、家庭护理质量等变量。我们试图找出治疗和结果之间的因果关系,同时考虑对于混杂者。(从技术上讲,我们不必考虑这些混杂因素,因为数据是通过随机试验收集的,任何由此产生的偏差都会被消除。但是,考虑到它们仍然是一个好主意,而且绝对是当数据是观察性的时,必须考虑它们)。
我们不关心 y_cfactual、mu0 和 mu1(它们被代码中链接的 GitHub 的创建者使用(一个关于因果效应变分自动编码器的超酷项目,或CEVAE,你应该完全检查一下))
If you’re interested in what they are:
y_cfactual is a counterfactual, which is a question about something that didn’t happen, like “What would happen if I…?” In this case, it's a prediction as to what would happen if there was, or was not, an intervention (depending on the context). **Counterfactuals are extremely important in causality because most of the times we aren’t always able to get all the data. **For example, if we wanted to test the effectiveness of two different treatments on a single person, we would not be able to test both of them. Counterfactuals address the “imaginary” treatment that did not actually get administered, and we, as humans, use counterfactuals all the time (every time you imagine an alternate situation). If you’re more interested about them, read this great blog post here.
Mu0 and mu1 are conditional means, in other words the expected or average value of y_factual with and without a treatment. The creators of the GitHub used these variables (y_cfactual, mu0, and mu1) to test the strength of the CEVAE.
Ok so now we have all the data setup, organized in a way that is convenient for causal inference. It’s time to actually do causal inference.
如果你对它们感兴趣:
y_cfactual 是一个反事实,这是一个关于没有发生的事情的问题,比如“如果我......会发生什么?” 在这种情况下,它是对有或没有干预(取决于上下文)会发生什么的预测。**
